CBSE 10th Result 2026

CBSE Class 10 Exams Time Table 2026

The Central Board of School Education (CBSE) has announced the dates for its Class 10 Annual Board Exams 2026, according to which the CBSE Class 10th Exam 2026 will be conducted from February 17, 2026 till March 11, 2026 and the Practical Exams 2026 are being held from January 01, 2026. The detailed subject-wise / day-wise CBSE 10th Date Sheet 2026 has been announced by the Board well before the exams. CBSE has also announced a rescheduling of exams which were earlier scheduled on 3rd March 2026 and the notice can be checked here: CBSE Exams Reschedule Notice 2026. Over 23 lakh candidates, from across the country & abroad, are likely to appear for the CBSE 10th Exam 2026. Students can keep visiting this page for the latest updates on the CBSE Board Exams 2026.

CBSE 10th Admit Card & Syllabus 2026

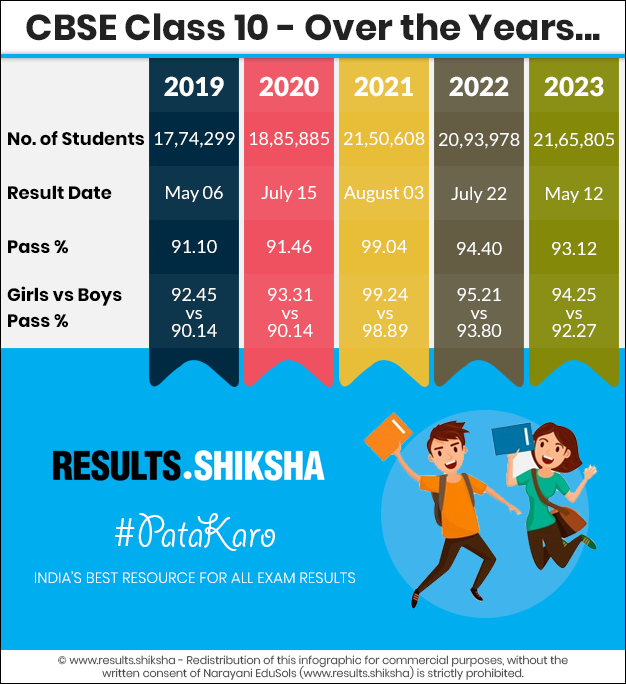
CBSE releases the CBSE Class 10 Admit Card by the end of January each year, with the exams commencing in February. The CBSE Admit Cards are released in the online mode at cbse.gov.in and parikshasangam.cbse.gov.in. Students are required to carry their CBSE 10th Admit Card 2026 on all the days of the examination. CBSE has also released its CBSE 10th Syllabus 2026 on its official website. Students appearing for the CBSE Class 10 exams are suggested to download the syllabus and refer to it regularly to prepare for the board examinations.

CBSE 10th Results Date 2026

The CBSE Class 10th Result 2026 is expected to be announced in May 2026 by the Central Board of Secondary Education (CBSE), given that the exams will be completed on 11th March 2026. In 2025, it was announced on 13th May for a total of 23,71,939 students and a pass percentage of 93.66 was recorded. With a 95 pass percentage, girls fared better than boys, who secured a 92.63 pass %. The passing criteria for CBSE Class 10 Exams is that the candidate must secure an overall 33% (including internal assessment and Class 10th Board examination) in all the subjects to pass. The result will be made available on the website - https://results.cbse.nic.in/ and cbse.gov.in and through www.results.shiksha.

CBSE 10th Result - Over the Years

Easy steps to check CBSE Class 10 Results 2026

Step 1: Go to CBSE Results 2026 Official Website: results.cbse.nic.in / www.cbseresults.nic.in or alternatively log on to https://www.results.shiksha/cbse/class-10.htm.

Step 2: Enter your CBSE 10th Roll Number 2026 / Admit Card ID / Date of Birth and click on the Get CBSE Results button.

Step 3: Your CBSE Class 10 Result & Marksheet 2026 will be displayed instantly.

Step 4: Take a printout of your CBSE 10th Result 2026 for future reference.